PANDANGAN ISOMETRIK

PENGENALAN

Lukisan pandangan isometrik bolehlah dianggapkan sebagai lukisan tigadimensi.

Ianya membantu untuk lebih memahami sesuatu rekabentuk objekdengan mudah. Pada pandangan – pandangan yang lain, biasanya objek dilukis dalam bentuk lukisan oblik, ortografik atau perspektif.

Bagi pandangan isometrik, objek dipegang condong pada suatu sudut. Dalam rajah 6.1 menunjukkan jenis – jenis pandangan sesuatu objek dalam lukisan kejuruteraan.

               (a) Pandangan Ortografik                                                   (b) Pandangan Isometrik

              (c) Pandangan Oblik                                                             (d) Pandangan Perspektif

Rajah 6.1 Jenis – jenis pandangan

HUBUNGKAIT LUKISAN ORTOGRAFIK DENGAN BENTUK OBJEK DALAM TIGA DIMENSI.

Lukisan ortografik adalah membantu untuk melukis pandangan isometriksupaya sesuatu objek sebenar dapat dilihat dan difahami dengan lebih mudah lagi. Dengan bantuan lukisan ortografik yang terdiri daripadapandangan pelan, hadapan dan sisi pandangan isometrik dengan mudahdapat digambarkan dan dilukiskan. Dalam rajah 6.3 menunjukkan lukisanortografik dengan bentuk dalam tiga dimensi. Semua contoh rajah dalam unit ini adalah unjuran sudut ketiga, kecuali jika dimaklumkan.

Rajah 6.3 Lukisan Ortografik dengan bentuk objek dalam tiga dimensi

KENALPASTI PERSAMAAN DAN PERBEZAAN ANTARA UNJURAN ORTOGRAFIK DENGAN PANDANGAN ISOMETRIK.

Di dalam lukisan kejuruteraan, unjuran ortografik dan pandangan isometrikadalah sangat memerlukan di antara satu dengan yang lain. Dengan itu,terdapat persamaan dan perbezaan di antara keduanya.

Persamaan di antara unjuran ortografik dengan pandangan isometrik.

Di antara persamaannya ialah unjuran ortografik mempunyai tiga pandangan iaitu pelan, hadapan dan sisi. Rajah 6.4 menunjukkan tiga pandangan dalam unjuran ortografik.

Rajah 6.4 Unjuran Ortografik mempunyai tiga pandangan

Dalam pandangan isometrik juga mempunyai tiga pandangan iaitu pandangan pelan, hadapan dan sisi. Rajah 6.5 di bawah menunjukkan pandangan isometrik yang dapat dilihat dari arah tiga pandangan.

Rajah 6.5 Pandangan Isometrik dari arah tiga pandangan

Perbezaan di antara unjuran ortografik dengan pandangan isometrik.

Di antara perbezaan yang dapat dilihat diantara unjuran ortografik dengan pandangan isometrik ialah objek yang sebenar. Di dalam unjuran ortografik, objek sebenar tidak dapat dilihat dengan jelas, kecuali pelukis yang mahir dalam teknikal sahaja yang dapat mengambarkan objek sebenar daripada unjuran ortografik. Rajah 6.6 menunjukkan unjuran ortografik yang hanya membayangkan objek sebenar.

Rajah 6.6 Unjuran ortografik dalam membantu melukis objek sebenar

Dalam pandangan isometrik, objek sebenar dapat dilihat denganmudah dan pandangan pelan, hadapan dan sisi dapat diperhatikan dengan jelas dalam membantu memahami objek sebenar itu lagi. Rajah 6.7 menunjukkan pandangan isometrik yang mengambarkan  suatu objek sebenar.

Rajah 6.7 Pandangan Isometrik yang mengambarkan objek sebenar.

KETANGENAN

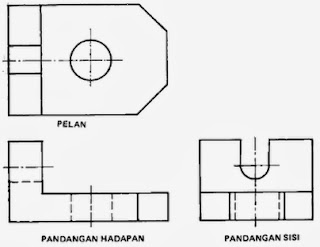
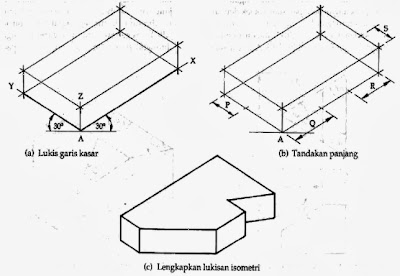
PENGENALAN

• Apabila satu garisan lurus bersentuhan dengan lengkok atau bulatan, garisan itu dikenal sebagai garisan tangen.
• Rajah 3.1(a) menunjukkan satu garisan lurus menyentuh bulatan. Titik dimana garis tangen menyentuh lilitan bulatan dinamakan titik sentuhan.
• Garisan yang menyambungkan pusat bulatan dengan titik sentuhan dinamakan garisan normal. Garisan normal berserenjang kepada garisan tangen.
• Ketangenan boleh juga berlaku di antara dua lengkok atau dua bulatan seperti yang ditunjukkan dalam rajah 3.1(b) dan 3.1(c) atau antara lengkok dua bulatan.
• Titik sentuhannya iaitu P dinamakan titik tangen. Rajah 3.1(b) menunjukkan dua bulatan yang menyentuh di sebelah luar, titk sentuhannya terletak pada garisan yang menyambungkan pusat bagi bulatan itu.
• Jarak di antara pusat bulatan ialah (R + r). Rajah 3.1(c) menunjukkan dua bulatan yang menyentuh di sebelah dalam.
• Titik sentuhannya terletak pada garisan yang menyambungkan pusat bulatan dan garisan itu dipanjangkan. Jarak di antara pusat bulatan itu ialah (R – r).

Rajah 3.1 (a) Satu garisan lurus menyentuh bulatan

Rajah 3.1(b) Dua bulatan yang menyentuh                    Rajah 3.1 (c) Dua bulatan yang menyentuh di sebelah luar                                      menyentuh di sebelah dalam

PEMBINAAN GARISAN TANGEN

Pembinaan garisan tangen dengan menggunakan jangkalukis dan peralatan lukisan yang lain.

Garisan Bertangen Kepada Bulatan atau Lengkok.

a) Membina tangen melalui titik T pada lilitan bulatan. 

Rajah 3.2 Membina tangen melalui titik T pada lilitan bulatan

Langkah – langkahnya.

• Lukis bulatan yang diberi pusatnya di P.
• Tandakan titik T di lilitan bulatan.
• Sambungkan PT dan panjangkan hingga ke R di mana TR = TP.
• Bahagi dua RP dan lukiskan tangen melalui titik T pada bulatan. XY adalah tangen yang dikehendaki.

(b) Membina tangen pada bulatan dari titik T

Rajah 3.3 Membina tangen pada bulatan dari titik T

Langkah – langkahnya.

• Lukiskan bulatan yang diberi pusatnya di P.
• Tandakan titik T yang diberi dan sambungkan T dan P.
• Bahagi dua garis TP di R.
• Berpusatkan R dan berjejarikan RT (RT=RP), lukiskan separuh bulatan memotong bulatan di X.
• Panjangkan TX hingga ke Y. TXY ialah tangen yang dikehendaki.

Garisan Bertangen Kepada Dua atau Lebih Bulatan/Lengkok.

(a)  Membina tangen luar diberi dua bulatan yang sama.

Rajah 3.4 Membina tangen luar diberi dua bulatan yang sama

Langkah – langkahnya

• Lukiskan dua bulatan yang diberi pada jarak yang dikehendaki.
• Sambungkan kedua-dua pusat T 1 dan T 2.
• Pada tiap-tiap pusat, bina garis tegak supaya memotong lilitan bulataan di titik sentuhan (titik tangen) M dan N. MN adalah tangen yang dikehendaki.
• Sambungkan MN.

(b) Membina tangen dalam pada dua bulatan yang mempunyai

      jejari sama.

* Garis T 2 S dan TT 2 adalah selari

Rajah 3.5 Membina tangen dalam pada dua bulatan yang mempunyai jejari sama.

Langkah – langkahnya:

• Lukiskan dua bulatan pada jarak yang dikehendaki.
• Sambungkan kedua-dua pusat bulatan T 1 dan T 2.
• Bahagi dua garisan T 1 T 2 di P.
• Bahagi dua garisan T 1 P di Q dan T 2 P di R.
• Dengan berpusatkan Q dan R , lukis bulatan uantuk mendapatkan titik persilangan S dan T. Garis ST adalah tangen dalam yang dikehendaki.

(c) Membina tangen luar pada dua bulatan , mempunyai jejari

      yang berbeza.

                        * Garisan T 1 R dan T 2 S adalah selari

Rajah 3.6 Membina tangen luar pada dua bulatan, mempunyai jejari yang berbeza

Langkah – langkahnya:

1. Lukiskan dua bulatan yang berjejari J1 dan J2 pada jarak yang dikehendaki.

2. Sambungkan kedua-dua pusat bulatan T 1 dan T 2 .

3. Bahagi dua garis T 1 T 2 di P.

4. Berpusatkan P dan berjejari PT 1 (PT 1 =PT 2 ), Lukiskan bulatan atau separuh

    bulatan.

5. Berpusatkan T 1 dan berjejarikan J1 – J2, , lukiskan bulatan yang memotong

    separuh bulatan di Q.

6. Sambungkan T 1 Q sehingga memotong bulatan besar di R, iaitu titik tangen pada

    bulatan besar.

7. Lukiskan T 2 S selari dengan T 1 R untuk mendapatkan titik tangen pada bulatan

    kecil. Garis RS adalah tangen yang dikehendaki.

(d) Membina tangen dalam pada dua bulatan yang mempunyai

      jejari yang tak sama.

Rajah 3.7 Membina tangen dalam pada dua bulatan yang mempunyai jejari yang tak sama

Langkah – langkahnya:

1. Lukiskan dua bulatan yang berjejari J1 dan J2 pada jarak yang dikehendaki.

2. Sambungkan kedua-dua pusat bulatan T 1 dan T 2 .

3. Bahagi dua garis T 1 T 2 di P.

4. Berpusatkan P dan berjejarikan PT 1 (PT 1 = PT 2 ), lukiskan separuh bulatan.

5. Berpusaatkan T 1 dan berjejarikan J1 + J2 , lukiskan bulatan yang memotong

    separuh bulatan di Q.

6. Sambungkan T 1 Q. Ia memotong bulatan besar di tangen titik R.

7. Lukiskan T 2 S selari dengan T 1 R untuk mendapatkan titik tangen S pada

    bulatan kecil. RS adalah tangen dalam yang dikehendaki.

Bulatan Bertangen kepada dua garis lurus.

(a) Membina satu bulatan bertangen kepada dua garisan menumpu dan menyentuh kepada satu titik yang diberi:

 Rajah 3.8 Membina satu bulatan bertangen kepada dua garisan menumpu dan menyentuh kepada satu titik yang diberi

Langkah-langkahnya:

1. Binakan garisan menumpu BA dan CA, dengan titik T pada garisan BA.

2. Bahagikan kepada dua sudut BAC.

3. Pada titik T binakan satu garis lurus bersudut tepat supaya memotong pada titik

    O.

4. Berpusatkan O dan berjejarikan OT , bina satu bulatan menyentuh ttitik T. Bulatan

    ini bertangen kepada dua garisan menumpu seperti dalam rajah 3.8.

(b) Membina satu bulatan bertangen kepada dua garisan

      menumpu diberi jejari bulatan.

Rajah 3.9 Membina satu bulatan bertangen kepada dua garisan menumpu diberi jejari bulatan

Langkah- langkahnya:

1. Bina garisan menumpu BA dan CA dengan jejari bulatan J diberi.

2. Bahagi dua sama sudut BAC dengan menggunakan jangka lukis.

3. Lukis dua lengkok di hujung garis CA dengan jejari J yang diberi.

4. Sambungkan puncak kedua-dua lengkok supaya memptong pada titik O.

    Berpusatkan O bina bulatan yang berjejarikan J supaya menyentuh dua garisan

    menumpu seperti dalam rajah 3.9.

(c) Membina bulatan bertangen kepada dua garisan menumpu

     serta melalui satu titik diberi di antaranya.

Rajah 3.10 Membina bulatan bertangen kepada dua garisan menumpu serta melalui satu titik diberi di antaranya

Langkah-langkahnya:

1. Diberi ialah dua garisan menumpu serta satu titik T di antaranya.

2. Bahagi dua sama buka sudut dua garisan menumpu dan sambungkan titik B

    kepada titik T.

3. Dari sebarang titik pada pembahagi dua sama sudut, lukiskan satu bulatan

    pusatnya X supaya menyentuh garis AB dan CB dan memotong pada titik Y.

    Sambungkan titik X Y.

4. Unjurkan garisan XY supaya selari melalui titik T dan memotong pada titik O.

    Berpusatkan titik O lukis bulatan supaya menyentuh titik T dan garisan AB dan CB

    seperti dalam rajah 3.10.

(d) Membina satu bulatan bertangen kepada bulatan diberi dan

     dua garisan lurus menumpu.

Rajah 3.11 Membina satu bulatan bertangen kepada bulatan diberi dan dua garisan lurus menumpu

Langkah- langkahnya:

1. Diberi ialah satu bulatan betangen kepada dua garis menumpu AB dan CB.

2. Bahagikan dua sama buka sudut garisan menumpu supaya memotong pada titik

    U dan Y, sambungkan TU. Melalui titik T bina garis bersudut tepat supaya

    memotong pada titik O, sambungkan TO.

3. Lukiskan XY selari dengan TU dan XZ selaari dengan TO.

4. Berpusatkan titik Z lukis bulatan jejarinya ZY supaya menyentuh bulatan diberi

    dan dua garis lurus menumpu (AB & CB) seperti dalam rajah 3.11.

PEMBINAAN LENGKUK BERTANGEN PADA DUA BULATAN

Anda telah pun membina garisan tangen kepada bulatan.

Pembelajaran kita seterusnya akan menyentuh pula satu lagi tangen iaitu lengkuk bertangen kepada bulatan.

Lengkok adalah sebahagian daripada bulatan. Lengkok biasanya digunakan bagi melukis komponen kejuruteraan dimana kebanyakaan binaannya terdiri daripada garisan lurus dan lengkok.

Lengkok-lengkok yang terdapat dalam komponen ini mungkin digunakan bagi mencantikkan bentuknya, ciri-ciri keselamatan, rekabentuk yang diperlukan bagi penggunaan semasa dan sebagainya.

Lengkok bertangen boleh dibahagikan kepada dua jenis iaitu, lengkok bertangen didalam bulatan dan lengkok bertangen diluar bulatan.

Lengkok Bertangen Pada Satu Bulatan.

a) Membina lengkok jejarinya r unit, yang bertangen didalam 

     satu bulatan, jejarinya R unit, pada titik P di lilitan bulatan.

    Langkah-langkahnya:

    1. Lukiskan bulatan yang diberi, pusatnya O.

    2. Tandakan titik P di garisan bulatan dan kemudian sambungkan

        OP.

    3. Dengan menggunakan O sebagai pusat dan jejari ( R - r ),

        lukiskan lengkok supaya menyilang di OP pada Q.

    4. Dengan menggunakan Q sebagai pusat dan jejari r unit, lukiskan

        lengkok yang dikehendaki seperti dalam rajah 3.12.

Rajah 3.12 Membina lengkok jejarinya r unit, yang bertangen didalam 
                     satu bulatan, jejarinya R unit, pada titik P di lilitan bulatan

b) Membina lengkok jejarinya r unit, yang menyentuh sebelah 

     luar bulatan, jejarinya R unit, pada titik P di lilitan bulatan.

    Langkah-langkahnya:

    1. Lukiskan bulatan yang diberi, pusatnya O.

    2. Tandakan titik P. Sambungkan OP dan panjangkan ke A.

    3. Dengan menggunakan O sebagai pusat dan ( R + r ) sebagai

        jejari, lukiskan lengkuk supaya menyilang OA pada S.

    4. Dengan menggunakan S sebagai pusat dan jejari r unit, lukiskan

        bulatan yang dikehendaki.

Rajah 3.13 Membina lengkok jejarinya r unit, yang menyentuh 
                     sebelah luar bulatan, jejarinya R unit, pada titik P di
                     lilitan bulatan

Lengkok Bertangen Pada Dua Bulatan

a) Membina lengkok diberi jejari bertangen dalam kepada dua

     bulatan yang diberi.

    Langkah-langkahnya:

   1. Lukiskan dua bulatan yang berjejari R dan r berpusat di A dan B .

   2. Diberi jejari lengkuk J.

   3. Berpusatkan dititik A, lukis lengkok jejarinya bersamaan dengan

       jejari bulatan ditolak dengan jejari J.

   4. Berpusatkan di titik B, lukis lengkok jejarinya bersamaan dengan

       jejari bulatan ditolak dengan jejari J supaya memotong pada titik

       O.

   5. Berpusatkan dititik O, lukiskan lengkok jejarinya J supaya

       menyentuh dua bulatan diberi seperti dalam rajah 3.14.

 Rajah 3.14 Membina lengkok diberi jejari bertangen dalam kepada 

                     dua bulatan yang diberi

b) Membina lengkok diberi jejari bertangen luar kepada dua  

    bulatan yang diberi.

    Langkah – langkahnya:

    1. Lukiskan dua bulatan yang berjejari R dan r berpusat di A dan B.

    2. Diberi jejari lengkok J.

    3. Berpusatkan dititik A lukis lengkok jejarinya bersamaan dengan  

        jejari bulatan ditambah dengan jejari J.

    4. Berpusatkan dititik B lukis lengkok jejarinya bersamaan dengan

        jejari bulatan ditambah dengan jejari J supaya memotong pada

        titik O.

    5. Berpusatkan dititik O, lukiskan lengkok jejarinya J supaya

        menyentuh dua bulatan diberi seperti dalam rajah 3.15.

Rajah 3.15 Membina lengkok diberi jejari bertangen luar kepada dua
                     bulatan yang diberi

PEMBINAAN LENGKOK PADA DUA GARISAN YANG BERSUDUT

Anda telahpun melukis lengkok bertangen kepada bulatan. Seterusnya anda akan melukis lengkok pada dua garisan yang bersudut. Terdapat tiga keadaan lengkok bertangen pada dua 

garisan iaitu lengkok bertangen kepada dua garisan menumpu dalam sudut tirus, lengkok bertangen kepada dua garisan menumpu dalam sudut cakah dan lengkok bertangen  

kepada dua garisan yang bersudut tepat.

Membina Satu Lengkok Bertangen Kepada Dua Garisan Menumpu Dalam Satu Sudut Tirus.

         Langkah- langkahnya:

        1. Lukiskan garisan menumpu AB, BC dalam buka sudut tirus 

            dan diberi jejari J. 

        2. Lukiskan satu garisan selari DE dengan garisan BC yang 

             jaraknya jejari J.  

        3. Lukiskan satu garisan selari FG dengan garisan AB yang 

             jaraknya jejari J supaya memotong pada titik O.

        4. Berpusatkan titik O lukis satu lengkok yang jejarinya J 

             supaya menyentuh dua garisan menumpu yang diberi 

             seperti dalam rajah 3.16.

Rajah 3.16 Membina satu lengkok bertangen kepada dua
                     garisan menumpu dalam satu sudut tirus

Membina Satu Lengkok Bertangen Kepada Dua Garisan Menumpu Dalam Satu Sudut Cakah.

         Langkah – langkahnya:

          1. Lukiskan garisan menumpu AB, BC dalam buka sudut 

               cakah dan diberi jejari J.

          2. Lukiskan satu garisan selari DE dengan garisan BC 

              yang jaraknya jejari J.     

          3. Lukiskan satu garisan selari FG dengan garisan AB yang 

               jaraknya jejari J supaya memotong pada titik O.

          4. Berpusatkan titik O lukis satu lengkok yang jejarinya J supaya 

              menyentuh dua garisan menumpu yang diberi seperti dalam  

              rajah 3.17.

Rajah 3.17 Membina satu lengkok bertangen kepada
                    dua garisan menumpu dalam satu sudut cakah

Membina Satu Lengkok Bertangen Kepada Dua Garisan Yang Bersudut Tepat.

Langkah – langkahnya:

1. Lukiskan garisan bersudut tepat AB, BC.

2. Berpusatkan dititik B bina satu lengkok dengan jejarinya J  

    supaya memotong pada titik D dan E.

3. Berpusatkan titik D, lukis satu lengkok jejarinya J.

    Berpusatkan dititik E juga lukiskan lengkok jejarinya J  

    supaya memotong pada titik O.

4. Berpusatkan dititik O lukiskan lengkok berjejari J supaya  

    menyentuh dua garisan bersudut tepat seperti dalam rajah  

    3.18.

Rajah 3.18  Membina satu lengkok bertangen kepada dua 

                     garisan yang berdudut tepat