GEOMETRI SATAH

PENGENALAN

Asas lukisan kejuruteraan ialah pembinaan garisan, sudut, bulatan, lengkok dan sebagainya. Lukisan ini dihasilkan dalam dua dimensi, iaitu yang mempunyai ukuran lebar dan tinggi. Dalam unit ini kita akan mempelajari pembinaan kotak tajuk dan garisan sempadan dengan garisan yang piawai diatas kertas lukisan. Kita juga akan melukis garisan , membina dan membahagi sudut tertentu dengan menggunakan alat-alat lukisan kejuruteraan. Selain itu juga kita akan melukis bentuk geometri mudah dengan pelbagai kaedah terhadap bentuk-bentuk berikut:

 i.  Bulatan

ii.  Segitiga

iii. Segiempat

iv. Poligon

v.  Elips

PEMBINAAN GARISAN & PEMBAHAGIAN SUDUT TERTENTU

Membina garisan selari.

Langkah – langkahnya:

    

• Satu garis AB dilukis.
• Dari sebarang dua titik pada garisan AB, dua lengkok dengan jejari yang sama dilukis.
• Selepas itu satu garis CD yang bersentuhan dengan kedua-dua lengkok dilukis.
• Akhirnya AB dan CD adalah dua garisan selari seperti dalam rajah 2.1.

Rajah 2.1 Membina Garis Selari

Membina garisan tegak.

Langkah – langkahnya:

i.   Satu garis AB dilukis.

ii.  Dari mana-mana titik ( C ), satu lengkok dibina yang memotong

     garisan AB di D dan E.

iii. Dari D, sebarang lengkok dibinadi atas dan di bawah AB.

iv. Dari E juga, sebarang lengkuk dibina yang sama memotong

     lengkok dari D.

v.  Akhirnya bina satu garisan dari titik C merentasi kedua-titik

     persilangan lengkuk seperti dalam rajah 2.2.

Rajah 2.2 Membina Garis Tegak

Membahagi dua garisan.

Langkah – langkahnya:

i.  Satu garis AB dilukis.

ii. Dari hujung A, sebarang lengkok dibina di atas dan di bawah
            garis AB.

iii. Dari hujung B juga satu lengkok dibina yang memotong lengkok A.

iv. Akhirnya garis yang memotong AB dari titik persilangan kedua-
              dua lengkok dibina seperti dalam rajah 2.3.

Rajah 2.3 Membahagi Dua Garisan

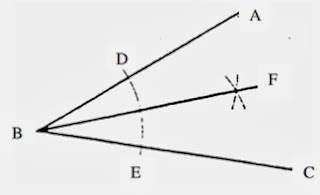
Membahagi dua sudut.

Langkah – langkahnya:

i.   Satu sudut ABC dilukis.

ii.  Dari B, satu lengkok dibina yang memotong AB dan BC di D dan E.

iii. Dari D, dengan jejari yang sama, satu lengkok dibina dan dari E

     juga, satu lengkok dibina yang akan memotong lengkuk dari D.

iv. Akhirnya satu garis dari titik B dibina kepada titik persilangan

     lengkok di F seperti dalam rajah 2.4.

Rajah 2.4 Membahagi Dua Sudut

Membahagi dua sudut yang terbentuk.

Langkah – langkahnya:

i. Satu garis AB dan CD adalah dua garis yang membentuk satu sudut.

ii. Langkah seterusnya, dua garis selari dibina di antara AB dan CD

    dimana garis FE selari dengan AB dan FG selari dengan CD.

iii. Selepas itu, sudut EFG dibahagikan kepada dua.

iv. Akhirnya FH adalah garis yang membahagi dua sudut tersebut

     seperti dalam rajah 2.5.

Rajah 2.5 Membahagi Dua Sudut Terbentuk

Membina sudut 60°

.

Langkah – langkahnya:

i.  Satu garisAB dilukis.

ii. Dari titik C, satu lengkok dibina yang memotong AB di D.

iii. Dari titik D, dengan jejari yang sama, satu lengkok dibina yang

     memotong lengkok dari C di E.

iv. Selepas itu, titik C dan E disambung.

v. Sudut ECB adalah sudut 60° seperti dalam rajah 2.6.

Rajah 2.6 Membina Sudut 60°

PEMBINAAN BENTUK GEOMETRI DENGAN BERBAGAI KAEDAH

Bulatan.

Membina bulatan melalui tiga titik yang diberi.

Langkah – langkahnya:

• Satu garis lurus dilukis yang menyambungkan A ke B dan B ke C.
• Garisan pembahagi dua sama bagi setiap garisan AB dan BC di bina supaya kedua-duanya bersilang di O.
• Dengan menggunakan O sebagai pusat jejari dan jejari OA, satu bulatan dilukis yang melalui titik A , B, dan C seperti dalam rajah 2.10.

Rajah 2.10 Membina Bulatan Melalui Tiga Titik Yang Diberi

Membina bulatan terterap dalam satu segitiga.

Langkah – langkahnya:

• Satu segitiga ABC dilukis.
• Selepas itu, kedua – dua sudut segitiga itu dibahagikan kepada dua bahagian yang sama dan akan bersilang di titik O.
• Dari O , satu garisan OP dilukis yang berserenjang kepada mana – mana satu sisi segitiga itu.
• Dengan menggunakan O sebagai pusat dan jejarinya OP, satu bulatan dilukis seperti dalam rajah 2.11.

Rajah 2.11 Membina bulatan terterap dalam satu segitiga

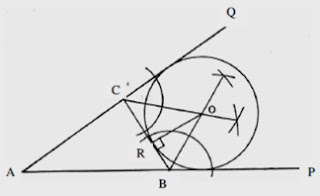
Membina bulatan terterap luar satu segitiga.

       

• Satu segitiga ABC dilukis.
• Selepas itu, garisan lurus AB dipanjangkan ke P dan garisan AC hingga ke Q.
• Selepas itu sudut PBC dan sudut BCQ dibahagikan kepada dua bahagian yang sama dan bersilang di O.
• Dari O, satu garisan OR dilukis yang berserenjang kepada sisi BC.
• Dengan menggunakan O sebagai pusat dan jejarinya OR, satu bulatan dilukis seperti dalam rajah 2.12.

Rajah 2.12 Membina bulatan terterap luar satu segitiga

Membina bulatan terterap lilit.

Langkah – langkahnya:

   

• Satu segitiga ABC dilukis.
• Selepas itu garisan AC dan BC dibahagikan kepada dua bahagian yang sama dan bersilang di O.
• Dengan menggunakan O sebagai pusat dan jejarinya OA, satu bulatan dilukis seperti dalam rajah 2.13.

Rajah 2.13 Membina bulatan terterap lilit

SEGITIGA.

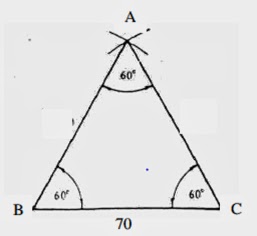
Membina segitiga sama diberikan ukuran sempadan.

Langkah – langkahnya:

• Satu garisan BC = 70 mm.
• Dari B, dengan jejari 70 mm, satu lengkok dibina pada garisan BC.
• Dari C, dengan jejari yang sama, satu lengkok lagi dibina yang memotong lengkuk dari B di A.
• Garisan BA dan AC disambungkan.
• Akhirnya ABC adalah satu segitiga sama seperti dalam rajah 2.14.

Rajah 2.14 Membina segitiga sama diberikan ukuran sempadan

Membina segitiga diberi ukuran tiap – tiap sempadan.

Langkah – langkahnya:

   

• Satu garisan AB = 80 mm dilukis.
• Dari A, dengan jejari 75 mm, satu lengkok dibina dari garisan AB.
• Dari A juga, dengan jejari 65 mm, satu lengkok lagi dibina yang memotong lengkok dari A di C.
• Garisan BC dan AC disambungkan.
• Akhirnya ABC adalah satu segitiga yang diberi sempadan seperti dalam rajah 2.15.

Rajah 2.15 Membina segitiga diberi ukuran tiap-tiap sempadan

Membina segitiga dua sisi sama diberi ukuran tapak dan ukuran tinggi.

Langkah – langkahnya:

• Satu garisan tapak AB = 60 mm.
• Garis tegak CD dibina tepat di garisan AB..
• Dari D, ketinggian 70 mm ditanda pada CD.
• Garis AC dan BC disambungkan.
• Akhirnya ABC adalah satu segitiga yang diberi ukuran tapak dan tinggi seperti dalam rajah 2.16.

Rajah 2.16 Membina segitiga dua sama sisi diberi ukuran tapak dan Tinggi ukuran

Membina segitiga diberi dua ukuran sempadan dan salah satu sudut tapak.

Langkah – langkahnya:

• Satu garisan tapak AB = 70 mm dilukis.
• Dari A, satu sudut BAX = 60° dibina.
• Dari A, jejari 60 mm, satu lengkok lagi dibina yang memotong lengkok dari AX di C.
• Titik B dan C disambungkan.
• Akhirnya ABC adalah satu segitiga yang diberi dua sempadan dan salah satu sudut tapak seperti dalam rajah 2.17.

Rajah 2.17 Membina segitiga diberi dua ukuran sempadan dansalah satu sudut tapak

Membina segitiga diberi ukuran tapak dan kedua-dua sudut tapak.

Langkah – langkahnya:

• Satu garisan tapak AB = 65 mm dilukis.
• Dari A, sudut BAY = 32° dilukis dengan menggunakan jangka sudut.
• Dari B, sudut ABX = 48° dilukis dengan menggunakan jangka sudut.
• Akhirnya kedua-dua binaan garisan tersebut akan bersilang di C.
• ABC adalah segitiga yang diberi ukuran tapak dan kedua-dua sudut tapak seperti dalam rajah 2.18.

Rajah 2.18 Membina segitiga diberi ukuran tapak dan kedua-dua sudut tapak.

Membina segitiga diberi ukuran tapak, ketinggian dan salah satu sudut tapak.

Langkah – langkahnya:

• Satu garisan tapak AB = 75 mm dilukis.
• Dengan berjejarikan ketinggian 60 mm, satu lengkok dibina di atas garis tapak AB dan satu garis selari dilukis di atasnya. 
• Dari A, satu sudut BAX = 70° dibina dengan menggunakan jangka sudut, yang mana akan memotong garisan selari di C.
• Titik B dan C disambungkan.
• Akhirnya ABC adalah satu segitiga yang diberi ukuran tapak, ketinggian dan salah satu sudut tapak seperti dalam rajah 2.19 

Rajah 2.19 Membina segitiga diberi ukuran tapak, ketinggian dan salah satu sudut tapak. 

SEGIEMPAT.

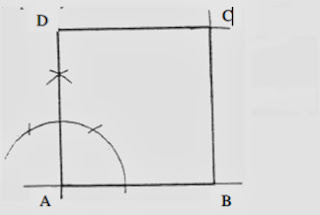
Membina segiempat sama diberi panjang sempadan.

Langkah – langkahnya:.

• Satu sempadan AB di lukis.
• Dari A, satu garisan tegak dibina.
• Berjejarikan AB, sempadan AD di tanda.
• Berpusatkan di B dan D dan berjejarikan panjang sempadan, lengkok-lengkok persilangan dibina pada C. 
• Akhirnya ABCD adalah segiempat sama seperti dalam rajah 2.20.

Rajah 2.20 Membina segiempat sama diberi panjang sempadan

Membina segiempat sama diberi pepenjuru. 

Langkah – langkahnya:

Satu pepenjuru PR yang diberi dilukis.

Seterusnya garis tengah PR dibina.

Dengan berjejarikan TP ( TP = TR ), TQ dan TS ditanda.

Seterusnya titik-titik tersebut disambung dan membentuk segiempat seperti dalam rajah 2.21.

 Rajah 2.21 Membina segiempat sama diberi pepenjuru

Membina segiempat bujur diberi pepenjuru dan salah satu sempadan.

Langkah – langkahnya:

• Satu pepenjuru PR dilukis.
• Seterusnya garis tengah PR dibina.
• Berjejarikan TP ( TP = TR ) dan berpusatkan T, satu bulatan dibina.
• Dengan berjejarikan panjang sempadan yang diberi, lengkuk dilukis yang memotong lilitan bulatan di Q dan S.
• PQRS adalah segiempat bujur seperti dalam rajah 2.22.

Rajah 2.22 Membina segiempat bujur diberi pepenjuru dan salah satu sempadan

Membina rombus diberi pepenjuru dan sempadan. 

      Langkah – langkahnya: 

• Satu pepenjuru PR dilukis.
• Dari P dengan berjejarikan ukuran sempadan yang diberi, satu lengkok dibina di atas dan di bawah supaya kedua – duanya bersilang di Q dan S.
• PQRS adalah rombus seperti dalam rajah 2.23.

 Rajah 2.23 Membina rombus diberi pepenjuru dan sempadan

Membina segiempat selari diberi dua sempadan dan satu sudut. 

Langkah – langkahnya:. 

      

• Salah satu sempadan yang diberi PQ dilukis
• Dari Q, satu sudut yang diberi dilukis. 
• Dengan panjang sempadan yang satu lagi ditandakan QR.
• Dari R, berjejarikan PQ, satu lengkok dilukis.
• Dari P, berjejarikan QR. Satu lengkok dilukis yang memotong lengkuk dari R di S.
• PQRS adalah segiempat selari seperti dalam rajah 2.24.

Rajah 2.24 Membina segiempat selari diberi dua sempadan dan satu sudut 

Membina sebuah trapezoid diberi sempadan-sempadan yang selari, tinggi tegak dan salah satu sudut.

Langkah – langkahnya:.

• Satu sempadan PQ dilukis.
• Dengan berjejarikan tinggi tegak trapezoid , lengkuk- lengkok dibina untuk mendapatkan garisan yang selari dengan PQ.
• Seterusnya sudut dibina dari Q supaya memotong yang selari dengan PQ di R.
• Akhirnya tandakan panjang RS yang diberi.
• PQRS adalah trapezoid seperti dalam rajah 2.25.

Rajah 2.25 Membina sebuah trapezoid diberi sempada-sempadan yang selari, tinggi tegak dan salah satu sudut

POLIGON

Membina segilima sama diberi ukuran sempadan.

Langkah – langkahnya:

• Satu sempadan AE dilukis.
• Garis AE tersebut dibahagikan kepada dua.
• Dari A, sudut 45° dibina supaya memotong garis tengah AE di 4.
• Dari E pula, sudut 60° dibina supaya memotong garis tengah AE di 6. 
• Selepas itu, garis antara 4 dan 6 dibahagikan kepada dua iaitu titik 5.
• Dengan berpusatkan titik 5, satu bulatan dibina yang menyentuh titik A dan E.
• Akhirnya dengan menggunakan jejari sempadan yang diberi, setiap sempadan ditandakan iaitu, A ke B, B ke C, C ke D dan D ke E sehingga membentuk segilima sama seperti dalam rajah 2.26.

Rajah 2.26 Membina segilima sama diberi ukuran sempadan

Membina segilima sama dalam sebuah bulatan diberi ukuran garispusat.

Langkah – langkahnya:

• Satu bulatan dilukis dengan garis pusat AP.
• Selepas itu, AP dibahagikan kepada bilangan mengikut sempadan segibanyak. Untuk segilima, ianya dibahagikan kepada 5 bahagian yang sama.
• Dengan menggunakan pusat P dan A, dan berjejarikan AP, sebarang lengkok dibina dan kedua - duanya akan bersilang di Q.
• Selepas itu, Q disambungkan ke nombor 2 sehingga memotong lilitan bulatan di B.
• Akhirnya AB adalah sempadan. Dengan menggunakan jejari AB, setiap sempadan ditandakan A ke B, B ke C, C ke D dan D ke E sehingga membina segilima seperti dalam rajah 2.27.

Rajah 2.27 Membina segilima sama dalam sebuah bulatan diberi ukuran garis pusat

Membina segienam diberi ukuran sempadan.

   

Langkah – langkahnya:

• Satu bulatan dilukiskan dengan berjejarikan sempadan yang diberi.
• Dengan berjejarikan sempadan tersebut, dari sebarang titik pada lilitan bulatan ditandakan kepada enam bahagian di sekeliling bulatan di A, B, C, D, E, dan F.
• Selepas itu, titik-titik A, B, C, D, E dan F disambungkan dan berakhir di A sehingga membentuk segienam sama seperti dalam rajah 2.28.

Rajah 2.28 Membina segienam diberi ukuran sempadan

Membina segienam diberi ukuran garis pusat.

Langkah – langkahnya:

• Satu bulatan dengan garis pusat yang diberi dibina.
• Dengan menggunakan sesiku 30°, garis sentuh dilukiskan kepada bulatan tersebut sehingga membentuk segienam sama.
• Akhirnya ABCDEF ialah segienam sama yang diberi ukuraan garispusat seperti dalam rajah 2.29.

Rajah 2.29 Membina segienam diberi ukuran garis pusat

Membina segitujuh sama diberi ukuran sempadan.

Langkah – langkahnya:

• Satu garis AB dengan ukuran sempadan yang diberi dilukis.
• Berpusatkan di B dan berjejarikan BA, separuh bulatan dilukis supaya bersilang di Q.
• Selepas itu, separuh bulatan itu dibahagikan pada jumlah bilangan sempadan poligon (180°/ 7).
• Dari B garisan ke 2 dilukis untuk membentuk sempadan yang seterusnya.
• Seterusnya AB dan B2 dibahagikan kepada dua supaya bersilang di P.
• Berpusatkan P dan berjejarikan PA satu bulatan dilukis.
• Akhirnya dengan ukuran AB, setiap sempadan ditanda sehingga membentuk segitujuh sama ABCDEFG seperti dalam rajah 2.30.

Rajah 2.30 Membina segitujuh sama diberi ukuran sempadan

Membina segilapan sama diberi ukuran pepenjuru.

Langkah – langkahnya:

• Satu bulatan dilukis yang bergaris pusatkan pepenjuru yang diberi iaitu AE.
• Garis tepat CG dibina dengan garis AE.
• Selepas itu keempat-empat sukuan dibahagikan kepada dua bahagian sehingga memotong lilitan bulatan di B, D, F, dan H.
• Selepas itu kesemua titik-titik A, B, C, D, E, F, dan G disambungkan sehingga membentuk segilapan seperti dalam rajah 2.31.

Rajah 2.31 Membina segilapan sama diberi ukuran pepenjuru

ELIPS

Membina elips dengan menggunakan dua bulatan pada satu pusat.

Langkah – langkahnya:

• Dua bulatan dilukis dengan jejari yang diberi pada satu pusat.
• Selepas itu, bulatan tersebut dibahagikan kepada 12 sektor yang sama.Ini bergantung kepada besarnya elips tersebut.
• Garisan-garisan pembahagi sektor itu akan memotong bulatan kecil dan bulatan besar.
• Seterusnya, garisan mendatar dan garisan menegak dilukis pada titik-titik persilangan tadi.
• Akhirnya, titik-titik persilangan antara garisan mendatar dan garisan menegak disambung sehingga membentuk elips yang lengkap seperti dalam rajah 2.32.

Rajah 2.32 Membina elips dengan menggunakan dua bulatan pada satu pusat.

Membina elips diberi segiempat tepat.

Langkah – langkahnya:

• Satu segiempat tepat dibina dengan panjangnya sebagai paksi besar dan lebarnya sebagai paksi kecil.
• Paksi besar dan paksi kecil tadi dibahagikan kepada bilangan yang sama.
• Seterusnya dari titik A dan B akan disambung kepada titik pembahagi paksi besar dan paksi kecil.
• Akhirnya titik – titik persilangan disambung sehingga membentuk sebuah elips seperti dalam  rajah 2.33.

Rajah 2.33 Membina elips diberi segiempat tepat

Membina elips diberi paksi besar dan paksi kecil.

Langkah – langkahnya:

• Satu paksi besar dan paksi kecil dibina iaitu CD dan AB.
• Selepas itu, separuh bulatan dilukis dengan berjejarikan ½ paksi besar dan berpusatkan di T. CA dan AD disambungkan.
• Berjejarikan AS, satu lengkok dibina yang memotong AC dan AD di E dan F.
• Selepas itu, CE dan FD dibahagikan kepada dua supaya memotong CT dan TD di G dan H serta bersilang di I.
• Berjejarikan IA, satu lengkok dibina diantara dua garisan pembahagi.
• Berjejarikan GC dan HD dan berpusatkan G dan H, satu lengkok dibina untuk melengkapkan separuh elips.
• Akhirnya langkah iii hingga vii diulang bagi melengkapkan elips yang separuh lagi seperti dalam rajah 2.34.

Rajah 2.34 Membina elips diberi paksi besar dan paksi kecil

Membina elips dengan gambarajah segiempat sama isometrik.

Langkah – langkahnya:

• Satu segiempat sama ABCD dibina yang diberi dalam pandangan isometrik.
• Keempat - empat sempadan segiempat dibahagikan dua di P, Q, R dan S.
• Berjejarikan BS ( BS = Br ) dan berpusatkan B, satu lengkok dibina dari S ke R, berjejarikan DQ ( DQ = DP ) dan berpusatkan D, satu lengkok dibina dari Q ke P.
• Akhirnya berpusatkan T dan U dan berjejarikan TP ( TP = TS ) dan UQ ( UQ = UR ) satu lengkok lagi dibina bagi melengkapkan bentuk elips seperti dalam rajah 2.35.

Rajah 2.35 Membina elips dengan gambarajah segiempat sama isometrik